Изучение таблицы умножения – нелёгкое дело. По-настоящему она «врастает» в голову только после нескольких лет практических вычислений. А на первых порах дети либо производят в уме несколько операций сложения, либо произносят мантру вроде «семь, четырнадцать, двадцать один, двадцать восемь…»
Эта статья не претендует на что-то революционное, но, тем не менее, может помочь освоить часть таблицы умножения, относящейся к числу 9. Итак, мы пользуемся десятичной системой счисления, то есть оперируем десятью цифрами. Девять – это десять минус один. Кроме того, мы знаем, что сумма цифр числа, делящегося на девять, тоже делится на 9. А в пределах таблицы умножения (от 1 до 10), сумма цифр равна девяти, то есть десяти минус один.
А теперь – методика. Положим перед собой руки. На руках десять пальцев. Один из них мы будем использовать, как разделитель.
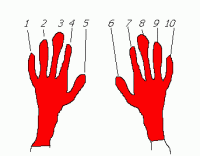 |
| Исходное положение |
Итак, например, девять умножить на три. Приподнимем (или согнем) третий палец – получается, что слева от разделителя 2 пальца, а справа – 7. Ответ – двадцать семь.
Так же можно провести умножение на любое число от одного до десяти. Если слева или справа от пальца-разделителя пусто – значит левая или правая цифра – ноль.
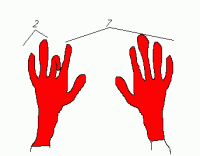 |
| Вычисление (учтите, я не художник) |
Эта методика позволит играючи освоить таблицу умножения на девять. А для продвинутых детей можно развить эту тему. Подобная методика годится для любой системы счисления. То есть, если мы пользуемся восьмеричной системой счисления, то благодаря данной системе мы легко освоим умножение на семь и при этом будем получать ответы в восьмеричном виде – 7, 16, 25 и т.д.
А вообще, последняя цифра в любой системе счисления несёт в себе особый смысл. Начиная от того, что сумма всех цифр числа делится на эту цифру, если число делится. В десятичной системе счисления этим свойством обладает не только девятка, но и тройка. А в семеричной, например?..
Кроме того, тот, кто знаком с десятичными дробями, знает, что такое дробь «в периоде». Например, число 0,(3) – это 0,333333333333333333333333333… , а 0,43(23) – это 0,432323232323….
Откуда берутся такие числа? Все очень просто.
Чтобы получить любое число «в периоде», надо поделить это число на число, имеющее столько же цифр, сколько и это число. Каких цифр? Ну, конечно же, девяток. Например, 53/99=0,5353535353…
Или 4898/9999=0,4898489848984898… Интересно?
Это правило относится к любой системе счисления, поэтому можно смело решить сложный пример в шестнадцатеричной системе счисления:
45АС/FFFF=0,45AC45AC45AC45AC45AC45AC45AC….
Но о системах счисления лучше поговорить потом, в другой статье…
А пока – удачи в освоении таблицы умножения.
Автор:



